Doppelsterne und ihr Bewegungsspiel
Die meisten Sterne unserer Milchstraße gehören Doppel- oder Mehrfachsystemen an (Beobachtungstipps). Die Komponenten umkreisen den gemeinsamen Schwerpunkt ihres Systems. Das kann innerhalb von Stunden von statten gehen. Dann jedoch wirbeln die Sterne in so geringer Distanz umeinander, dass wir sie im Teleskop nicht auflösen können. Wir sehen deren gemeinsames Leuchten als einen einzigen Lichtpunkt.
Bei Doppelsternen mit Umlaufszeiten von vielen hundert Jahren ist das oft anders: Sie trennt das Teleskop sehr wohl in zwei oder mehrere Komponenten. Der Anblick kann überaus hübsch sein, weshalb solche Systeme von Amateurastronomen immer wieder gern ins Visier genommen werden.

Bloß ein Spiel der Perspektive?
Lange glaubte man, solche Sterne stünden nur zufällig in fast der gleichen Blickrichtung, wären in Wirklichkeit aber weit voneinander entfernt: Der hellere Stern stünde uns einfach näher als der schwächere.

Wilhelm Herschel.
Aus: Wilhelm Meyer, Weltgebäude (1914)
Aus: Wilhelm Meyer, Weltgebäude (1914)
Das dachte zunächst auch Wilhelm Herschel. Er sammelte Doppelsternbeobachtungen, um die damals noch nicht nachgewiesene Fixsternparallaxe zu bestimmen.
1802 hatte Herschel schon 700 Sterne als Doppelsterne entlarvt. Etliche musterte er nun, nach zwei Jahrzehnten, wieder. Dabei erkannte Herschel: Bei einigen hatte sich die Position der schwächeren Komponente relativ zur helleren verändert - und zwar in einer Weise, die einen Umlauf andeutete!
1802 hatte Herschel schon 700 Sterne als Doppelsterne entlarvt. Etliche musterte er nun, nach zwei Jahrzehnten, wieder. Dabei erkannte Herschel: Bei einigen hatte sich die Position der schwächeren Komponente relativ zur helleren verändert - und zwar in einer Weise, die einen Umlauf andeutete!
Besonders eng mit Herschel ist der Stern Xi Ursae Majoris verwoben. Der deutschstämmige, nach England ausgewanderte Astronom sah dessen Begleiter erstmals 1780.
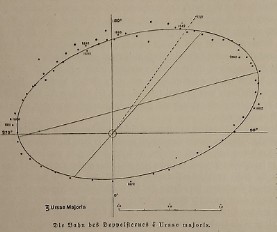
Der Umlauf von Xi Ursae Majoris.
Aus: Wilhelm Meyer, Weltgebäude (1914)
Aus: Wilhelm Meyer, Weltgebäude (1914)
22 Jahre später war er sich dessen Bewegung sicher. Damit war die Existenz physischer Doppelsterne bewiesen: Diese Sonnen sind gravitationell aneinander gebunden, umkreisen einander.
Im Fall von Xi Ursae Majoris dauert ein Umlauf, wie der französische Astronom Félix Savery 1827 zeigte, 60 Jahre.
Newtons Gravitationsgesetz galt also auch weit außerhalb des Sonnensystems.Bis dahin hatten etliche Astronomen gemeint, alle Sterne besäßen in etwa die gleiche Leuchtkraft. Ihre unterschiedliche Helligkeit am irdischen Himmel käme nur durch deren unterschiedliche Erddistanz zustande.Doch weil sich die beiden Komponenten eines physischen Doppelsternsystems die selbe Erddistanz teilten, mussten krass unterschiedliche Helligkeiten im Telekop von höchst verschiedenen Leuchtkräften bedingt sein. Es gab also höchst unterschiedliche Sonnen im All. Giordano Bruno (Artikel) hatte dies schon um 1585 behauptet. Jetzt erst war es bewiesen.
Wir dürfen das miterleben
Wir können das alles nachprüfen - mit dem Auge am Teleskop und einem Messokular (visuelle Astrometrie) oder mit Hilfe der fotografischen Astrometrie.Dabei fertigen wir hoch auflösende Fotos von interessanten Doppelsternen an. Daraus ermitteln wir zwei Größen:
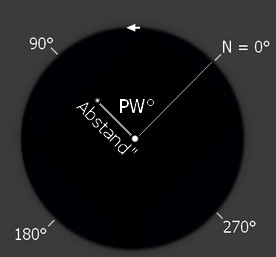
- den Abstand der beiden Komponenten in Bogensekunden
- den Positionswinkel der schwächeren zur helleren Komponente in Grad
Nach möglichst vielen Jahren fertigen wir wieder eine Aufnahme an, ermitteln Abstand und Positionswinkel erneut. Da wir die Ergebnisse in absoluten Zahlen ausdrücken, dürfen wir sogar Teleskop und Kamera wechseln.
Der Umlauf der Komponenten um den gemeinsamen Schwerpunkt drückt sich in der Veränderung beider Größen aus.Damit ist uns dann auch der Nachweis gelungen, es hier mit einem physischen Doppelstern - und nicht bloß mit einem Spiel der Perspektive - zu tun zu haben.
Der böse Spiegel
Der Kameraspiegel führt bei kurz belichteten Fotos zu Erschütterungen, die das Sternbildchen nach "oben" bzw. "unten" verformen. Um das zu vermeiden, sollte man die Spiegelvorauslösung aktivieren. In APT stellt man dazu die Anti Vibration Pause im Register Cam z.B. auf 4 Sekunden ein und lässt die Steuersoftware dann einen Lightframe-Plan mit kurzen Belichtungszeiten abarbeiten.Alternativ wählt man die APT-Funktion Shoot, wobei die Belichtungszeit zuerst auf Bulb gestellt und unter Bulb Seconds z.B. 1/5 wählt. Auch dann lässt sich die Anti Vibration Pause nutzen.
Bei welchen Sternen lohnt es sich besonders?
Grundsätzlich kann man jeden auflösbaren Doppelstern astrometrieren. Besonders spannend ist die Sache aber freilich dort, wo man wirklich Veränderungen mitverfolgen kann.Wolfgang Vollmann gibt auf seiner Website einige Doppelsterne an, bei denen das Bewegungsspiel in vergleichbar kurzer Zeit auffällt:
- Eta Cassiopeiae
- Alpha Canis Maioris (sehr schwierig zu trennen)
- Alpha Geminorum
- Zeta Cancri
- Xi Ursae Majoris (siehe oben)
- Gamma Virginis
- Xi Bootis
- Eta Coronae Borealis
- 70 Ophiuchi
- 61 Cygni
- Krüger 60 Cephei
Wolfgang Vollmann beschreibt auf seiner Website sehr anschaulich, wie hier verfahren wird. Ihm verdanke ich vor allem den Tipp, jeweils zwei unterschiedlich lang belichtete Aufnahmen anzufertigen.
Der einfachste Fall - eine einzige Aufnahme
Die Komponenten der in Frage kommenden Doppelsterne stehen in der Regel sehr eng beisammen. Man wird also Teleskope mit hohen Brennweiten und nach Möglichkeit Kameras mit kleinen Pixeln vorziehen. Das Bildfeld darf aber auch nicht zu sehr schrumpfen - sonst fehlen der Software später die Anhaltssterne zum Vermessen.
Ich schieße Aufnahmen mit möglichst kurzer Belichtungszeit: Sie sollen die schwächere Komponente gerade noch erfassen, ohne die hellere "ausufern" zu lassen. Ideal wären zwei klar definierte Punkte, wie sie allerdings nur bei ähnlich hellen Komponenten möglich sind. Ist auch ein halbes Dutzend Vergleichssterne am Foto auszumachen - sehr gut! Dann wird man die Aufnahme später leicht vermessen können.Man ermittelt die absoluten äquatorialen Koordinaten beider Komponenten und berechnet daraus ihren gegenseitigen Abstand in Bogensekunden und den Positionswinkel. Für den Abstand reicht der Satz des Pythagoras aus (die Differenz in Rektaszension muss aber mit dem Cosinus der Deklination der helleren Komponente multipliziert werden). Zur Bestimmung des Positionswinkels braucht man ein wenig Trigonometrie. Man zählt ihn vom Norden her gegen den Uhrzeigersinn!

Ein Beispiel:Am 10.2.2022 fotografierte ich Sirius B mithilfe einer quadratischen Maske vor dem Objektiv. Er "klebt" geradezu an der gleißenden Komponente A, uns als Sirius vertraut. ASPS konnte mit dem Bild nichts anfangen, PlateSolve2 hingegen schon. Der batzige Sirius war denkbar schwer zu vermessen, der Weiße Zwerg Sirius B relativ leicht. Aus den so ermittelten äquatorialen Koordinaten beider Sterne berechnet sich deren gegenseitiger Abstand:Sirius A
RA 06h45m07,84s DE -16°45'08,52" (2000)
Sirius B
RA 06h45m08,52s DE -16°43'21,1" (2000)
Ermittelter Abstand: 10,7'' - PW: 65,8°Zum Vergleich GUIDE: 11,3" - PW 64,4°Angesichts der schwierigen Bedingungen bin ich mit dem Ergebnis sehr zufrieden.
Mit zwei Fotos zum Ziel
Oft wird man es nicht schaffen, die Doppelstern-Komponenten möglichst klein zu halten und dennoch genügend Anhaltssterne für die Astrometrie-Software aufs Bild zu bekommen. Dann braucht man zwei Fotos: ein möglichst kurz belichtetes für die Komponenten und ein länger belichtetes für die Vergleichssterne.
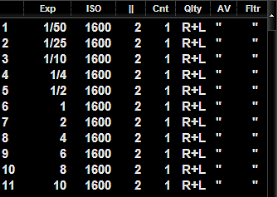
Mit einer Belichtungsreihe werden die optimalen Belichtungszeiten für die beiden geeigneten Fotos ermittelt. Mit der Software APT geht das besonders bequem, da man einen entsprechenden "Plan" abspeichern und wiederholt aufrufen kann.
Wir wollen bestimmte Daten von der einen in die andere Aufnahme übertragen. Bei einer parallaktischen Montierung, auch äquatoriale Montierung genannt, ist das einfach. Hier ändert sich der Winkel der Kamera zum äquatorialen Koordinatensystem nur durch Unzulänglichkeiten. Bei einer azimutalen Montierung (auch alt-azimutale Montierung genannt) geschieht dies aber ständig, von der kurzen Zeit des Meridiandurchgangs einmal abgesehen.Bei einer azimutalen Montierung müssen die kurz- und die langbelichtete Aufnahme sehr rasch hintereinander geschossen werden, ohne irgendetwas am Fernrohr oder der Kamerastellung zu verändern. Nur die Nachführung bleibt aktiv.Der Luftunruhe wegen empfiehlt es sich, von der kurzbelichteten Aufnahme gleich mehrere Versionen anzufertigen. Man sucht dann jene mit der punktähnlichsten Sternabbildung heraus.

Das langbelichtete Foto (links ein Ausschnitt mit Zeta Cancri) wird nun astrometriert. Dabei geht es uns jetzt ausnahmsweise nicht um die äquatorialen Koordinaten der Sterne, sondern eigentlich um zwei Nebeninformationen, die die Software liefert:
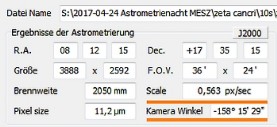
Den Abbildungsmaßstab (wieviele Winkelsekunden repräsentiert jedes Pixel) und die Drehung des Bildfelds relativ zum äquatorialen Koordinatensystem.
PlateSolve2 liefert die Bildfelddrehung gleich in weiter verarbeitbarer Weise. Der All Sky Plate Solver (siehe obiges Bild) zählt anders. Da muss man 180 Grad addieren.Das oben gezeigte Foto von Zeta Cancri wurde übrigens 10 Sekunden lang belichtet.

Nun nehmen wir uns das kurzbelichtete Foto (hier eines mit 1/30 sec Belichtungszeit) vor, das die beiden Doppelstern-Komponenten möglichst "punktähnlich" zeigt.
Wir öffnen es in einem passenden Fotobearbeitungsprogramm. Ich schaue mir die beiden Sternscheibchen mit einer Bildschirmvergrößerung von 300 oder 400-fach ("Zoom") an - siehe Foto oben. Dann bearbeitete ich das Foto mit den Reglern Schärfen, Helligkeit, Kontrast und Gamma, bis sich die beiden hellsten Pixel in jedem Scheibchen herauskristallisieren - wie auf dem Foto oben.
Variante 1: Zwei Fotos und der digitale Winkelmesser
Wir benötigen dazu ein Fotobearbeitungsprogramm, bei dem man Distanzen und Winkel messen kann. Beim kostenlosen GIMP ruft man dazu unter "Werkzeuge" das Maßband aus und zieht eine Linie von der hellen zur schwächeren Komponente. Ganz unten sieht man dann die Distanz in Pixeln und den Winkel.
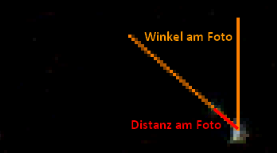
Multipliziert man die Distanz in Pixeln mit dem Maßstab, den wir aus dem langbelichteten Foto gewonnen haben, erhalten wir die Distanz der beiden Komponenten in Bogensekunden.
Der Winkel wird (zumindest bei GIMP) sehr eigenwillig gemessen. Er ist dort immer nur auf den jeweiligen Quadranten bezogen. Da heißt es aufpassen, mitdenken und umrechnen. Wir wollen jedenfalls einen Wert, der von oben gegen den Uhrzeigersinn gezählt wird.Nun bringen wir noch den Drehwinkel aus dem langbelichteten Foto in Rechnung, um den Winkel aus dem kurzbelichteten Bild ins äquatoriale System zu bekommen. Wird das Ergebnis negativ, addieren wir 360 Grad. Übersteigt es 360 Grad, ziehen wir die Zahl 360 ab.
Variante 2: Zwei Fotos und Pixelkoordinaten
Ich mag die Winkelmesserei am Bildschirm nicht und ziehe eine etwas andere Methode vor: Programme wie PlateSolve2, IRIS, GIMP und viele andere Fotobearbeitungsprogramme zeigen bei jedem Punkt, den wir mit dem Mauszeiger berühren, zwei Zahlenwerte an: Eine Pixelkoordinate in waagrechter x-Richtung und eine Pixelkoordinate in senkrechter y-Richtung.Gemessen wird parallel zu den Bildkanten, allerdings misst IRIS z.B. von links unten weg, während PlateSolv2 und GIMP den Nullpunkt links oben setzen.
Für jede der beiden Doppelstern-Komponenten, den Hauptstern und den Begleiter, erhalten wir jedenfalls zwei Pixelkoordinaten.
Auch hier ermittet man mit dem Satz von Pythagoras den diagonalen Abstand in Pixeln (ohne Multiplikation mit dem Cosinus!). Multiplizieren wir den Pixel-Abstand am Foto mit dem Maßstab aus dem langbelichteten Foto, kennen wir die Distanz der beiden Sterne am Himmel - in Winkelsekunden.Mithilfe der Trigonometrie errechnen wir nun den Winkel der beiden Komponenten am Foto, mit dem helleren Stern im Scheitel. Um den Positionswinkel am Himmel auszurechnen, müssen wir noch den vom länger belichteten Foto bekannten Drehwinkel in Rechnung stellen.
Excel und Co. helfen
Mit Hilfe eines passenden Excel-Sheets (man kann freilich auch eine andere Software mit Tabellenkalkulation nützen) lassen sich die oben angerissenen Rechenvorgänge automatisieren. Allerdings muss man bedenken, dass Excel bei Winkelfunktionen nicht im Gradmaß, sondern im Bogenmaß rechnet (360 Grad im Gradmaß entsprechen 2*Pi im Bogenmaß).
Man kann es übrigens gleich so programmieren, dass es automatisch den Mittelwert der Ausmessungen von mehreren, sofort hintereinander geschossenen Fotos bildet. Das spart Zeit und sollte die Genauigkeit erhöhen.
Beispiel Zeta Cancri (A-C)
Wie oben schon gezeigt, verwendete ich zur Vermessung des Doppelsterns Zeta Cancri (Komponenten A und C) zwei Fotos: mit 1/30 sec und 10 Sekunden Belichtungszeit. Die langbelichtete Aufnahme zeigte genug Vergleichssterne, damit der All Sky Plate Solver den Maßstab (0,563) und die Drehung des Bildfelds (-158°14'26") in Relation zum äquatorialen Koordinatensystem errechnen konnte. Die Kamera war somit um 21,8° im Uhrzeigersinn verdreht.

Mit meinem Fotoprogramm schärfte ich die Pixel der beiden Komponenten nach und erhielt die Wertepaare x=2079 und y=1020 für die helle sowie x=2072 und y=1013 für die schwächere Komponente. Die Differenzen der x-Werte (7) und der y-Werte (hier ebenfalls 7) wurden quadriert und dann addiert. Die Wurzel daraus ergibt den Pixelabstand 9,9. Mit dem obigen Maßstab multipliziert, erhalte ich eine Distanz der beiden Sterne von 5,6".Aus dem Verhältnis der beiden Differenzen ergibt sich der Winkel am Foto: 45° (von oben und gegen den Uhrzeigersinn gemessen). Weil die Kamera aber um 21,8° im Uhrzeigersinn verdreht war, muss ich sie mathematisch um eben diesen Betrag gegen den Uhrzeigersinn rotieren lassen: 45° + 21,8° = 66,8°. Das ist der Positionswinkel (PW).Das Resultat dieser Astrometrierung lautet daher:
Zeta Cancri (Komponenten A und C)Abstand: 5,6" (5,9")PW: 66,8° (65,2°)Termin: 2017,3. Epoche: J2000
Die Werte in Klammer habe ich zum Vergleich berechnet:mit meinem alten Basic-Programm und einem Auszug aus Bahnelementen des Aitken Double Star Catalogue.
Beispiel Rigel, Orion
Der Doppelstern ist visuell schwierig aufzulösen, geschweige denn zu vermessen. Aus einem lang- (3s, ISO 12800) und einem kurzbelichteten Foto (1s, ISO 100) sofort danach errechnet sich: 9,7" / 205,6°
(Termin: 2024,1; Epoche J2000)Offizielle Werte: 9,5" / 204°

Vergleichsdaten für Doppelsterne
Um die Daten der eigenen Astrometrie zu überprüfen und zu vergleichen, gibt es mehrere Möglichkeiten.
Vergleich mit aktuellen Angaben zu Positionswinkel und Distanz
- Manche Desktop-Planetarien sowie (meist teure) Programme zur Planung von Beobachtungsnächten berechnen wohl die aktuellen Daten angeklickter Doppelsterne und zeigen diese an.
- Die sehr empfehlenswerte Website Stelle Doppie von Gianluca Sordiglioni macht aktuelle Angaben zu zahlreichen Doppelsternen. Sie können eine Auswahl nach verschiedensten Kriterien treffen und sogar eigene Beobachtungen hochladen. Außerdem liefert Ihnen diese Site auch die orbitalen Elemente von Doppelsternen (hier grundsätzliches dazu von Bruce MacEvoy).
- Falls Sie die orbitalen Elemente kennen, können Sie die aktuellen Angaben selbst berechnen bzw. berechnen lassen. Die Elemente ausgewählter Doppelsterne finden Sie auch auf einer Seite von Ian Ridpath. Zur Berechnung bietet er ein BASIC-Programm an (bei Win7 ist BASIC über den Emulator DOS-Box reaktivierbar). Roger Wesson offeriert hingegen ein online-Skript zur Berechnung. Ähnliches macht auch Albireo, wenngleich für hinterlegte Elemente aus einer internen Datenbank.
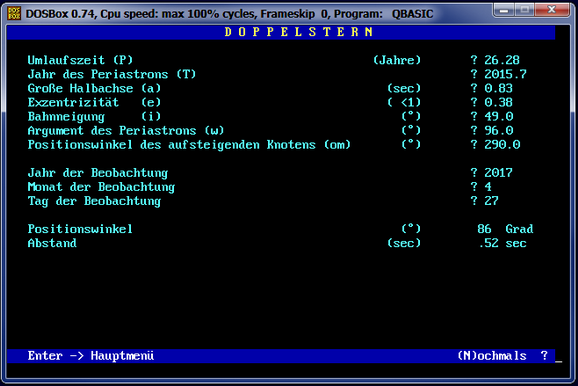
Vergleich mit älteren Angaben zu Positionswinkel und Distanz
- Bei Doppelsternen mit langen Umlaufszeiten bleiben ältere, also nicht aktualisierte Angaben aktuell genug. Versuchen Sie es online mit The Washington Visual Double Star Catalog. Außerdem zeigt Richard Dibon-Smith auf seiner Website die Orbits von 150 Doppelsternen.
- Etliche Astronomiebücher und -zeitschriften informieren ebenfalls über Doppelsterne. Mehr als 2000 Doppelsterne stellt Sissy Haas in "Double Stars for small Telescopes" vor. Ähnlich viele enthält The Cambridge Double Star Atlas. Einer der Autoren, Bruce MacEvoy, stellt auf seiner Website mehrere Data Sets als Excel-Sheets bereit. Auf eine wesentlich kleinere Auswahl beschränkt sich Klaus M. Schittenhelm im Buch "Sterne beobachten in der Stadt".
Castor: Bewegung nachgewiesen?
Möglicherweise ist es mir hier zum ersten Mal selbst mit den Mitteln der fotografischen Astrometrie gelungen, die Bewegung einer Doppelstern-Komponente nachzuweisen.
- Castor 2017,32: 5,3" 52.8°
- Castor 2020,39: 5,6" 50,7°
- Castor 2024,12: 6,0" 47,7°
Die Abstände werden von meiner Anordnung etwas überschätzt, aber die Tendenz passt nach 6,8 Jahren zu den theoretischen Daten: Der Abstand der Komponenten nimmt auch bei meinen Messungen zu, der Positionswinkel verringert sich ebenfalls.
Die Umlaufszeit soll 467 Jahre betragen. Der Minimalabstand stellte sich 1957 ein. Übrigens galt Castor in meiner Jugendzeit mit etwas über 2" Abstand als visuell eher schwer zu trennen. Heute ist das deutlich einfacher. Allerdings besaß mein Teleskop damals auch nur 60 mm Öffnung.

Weiter zu: Eigenbewegung der Sterne
Alle Angaben ohne Gewähr. Ich übernehme keine Haftung für die Inhalte anderer Sites, auf die sich Links meiner Website richten.
