Fixsternparallaxe - Sterndistanzen - Dr. Christian Pinter - Fototipps

Schon Galileo Galilei sehnte sich danach, eine Fixsternparallaxe nachzuweisen. Diese periodische Winkelverschiebung ist nämlich nichts anderes, als die Widerspiegelung der Erdbewegung um die Sonne. Und eine solche Bewegung zu lehren, war ab 1616 in den katholischen Ländern verboten!

Als Castelli den Stern Mizar im Großen Bären als Doppelstern entlarvte, machte er seinem Freund Galilei Mitteilung. Und zwar 1617, per Brief. Aus Angst, die Zensur könnte auch  dieses Schreiben abfangen, vernebelte Castelli den Fund und die erhofften Perspektiven jedoch. Ich zitiere ihn sinngemäß: Der Stern Mizar ist eines der schönsten Dinge am Himmel. Ich glaube, nichts könnte unserer Sache besser dienen.

Lange Zeit eigneten sich Teleskope nur sehr bedingt als Messgeräte. Was immer man probierte: Die winzige Parallaxe war nicht nachzuweisen.

Dass man die Fixsternparallaxe im 17. Jh. nicht nachweisen konnte half dem Vatikan, die von Kopernikus postulierte Erdbewegung zu leugnen.

Herschel erstellte einen Katalog mit 700 Doppelsternen, um weiterhin nach der Fixsternparallaxe zu suchen. Schließlich fand er heraus: Etliche dieser Objekte waren gar keine optischen, sondern physische Doppelsterne. Sie standen aus unserer Perspektive nicht nur zufällig in der gleichen Richtung, sondern umkreisten einander tatsächlich.

Wieder war Herschel eine bedeutende Entdeckung geglückt!

Erst 1838 sollte es Friedrich Bessel in Königsberg gelingen, eine sichere Fixsternparallaxe nachzuweisen. Da die Größe der Parallaxe mit zunehmender Sterndistanz abnimmt, ließ sich so erstmals auch eine verlässliche Sterndistanz ermitteln - und zwar am Stern 61 Cygni (Foto links).

Das Foto rechts zeigt jene Publikation, die Kunde von der Entdeckung gab. Bessel verwendete dazu ein Heliometer aus der Werkstatt Joseph Fraunhofers, also ein Spezialteleskop mit geteilter Objektivlinse. Es erlaubte extrem genaue Winkelmessungen.

Später wurde das weltgrößte Heliometer in der Kuffner-Sternwarte (Foto rechts), Wien-Ottakring, installiert - mit einem Linsendurchmesser von 22 cm.

Damit vermaß man schließlich 16 Fixsternparallaxen und somit 16 neue Sterndistanzen.

Das waren vergleichsweise viele Resultate, da bis 1908 weltweit nicht einmal hundert derartige Messergebnisse vorlagen.

Wir dürfen unser Teleskop unbeschadet lassen und setzen statt dessen eine Kamera in seinen Fokus. Mit großer Teleskopöffnung und kleinen Pixeln im Sensor gelingen uns hochauflösende Aufnahmen. Die sind auch nötig, haben wir es hier doch mit extrem winzigen Winkeln zu tun: Die gesuchte Parallaxe (p) ist in jedem Fall kleiner sind als 1 Bogensekunde!

Eine Bogensekunde ist der 3600. Teil eines Winkelgrads bzw. der 1800. Teil der Vollmonddurchmessers. Um die Dimension klar zu machen: Unter diesem winzigen Winkel erschiene uns ein Mensch in 350 km Entfernung. Das ist die Distanz von Wien nach München.

Bei ruhiger Luft und unter Einsatz statistischer Verfahren schaffen wir mit 200 mm Öffnung, 2.000 mm Brennweite und Sensorpixeln um 3 bis 4 Mikrometer mitunter sogar eine halbe Bogensekunde Messgenauigkeit. Das entspräche dann der Distanz Wien - Danzig bzw. der Entfernung von Wien nach Frombork; jenem Ort, wo Kopernikus einst sein epochales Hauptwerk De Revolutionibus schrieb.

Die jährliche Fixsternparallaxe (p) ist jener Winkel, unter dem ein Beobachter auf dem fraglichen Stern den Radius (!) der Erdbahn erblicken würde.

Daher sind zwei Messungen nötig. Terminlich bieten sich zwei Möglichkeiten an.

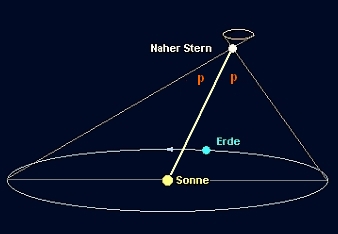
Nach seiner Konjunktion mit der Sonne taucht ein Stern zuerst am Morgenhimmel auf, ist später zur Oppositionsstellung die ganze Nacht über sichtbar und zieht sich später an den Abendhimmel zurück - bevor er wieder der Konjunktion mit der Sonne zustrebt und unbeobachtbar wird.

Messen im Abstand von 6 Monaten

Messen im Abstand von 3 Monaten

Den genaueren Wert sollte man natürlich bekommen, wenn man im Abstand von 6 Monaten astrometriert und das Ergebnis halbiert.

Nebenbei erbringen wir damit auch einen Beweis für die jährliche Bewegung der Erde um die Sonne. Galilei hätte sich gefreut, über unsere heutigen Möglichkeiten zu verfügen.

Die entsprechenden Aufnahmen werden astrometriert, die Ergebnisse zusammen mit Datum und Uhrzeit abgelegt. Am besten, man hebt in diesem Fall auch das Foto auf, um es später bei Bedarf nochmals ausmessen zu können.

Danach rechnet man vom äquatorialen ins ekliptikale Koordinatensystem um. Wer sich die Rechnerei sparen will, kann das Programm KStars einsetzen - eigentlich ein mächtiges Freeware-Desktop-Planetarium (Menü Extras / Rechner / Koordinatenkonverter / Ekliptikale Koordinaten). Denn interessant ist die durch die Parallaxe bedingte Verschiebung der Sternposition in ekliptikaler Länge (in Bogensekunden).

Diese ist im Idealfall die gesuchte Parallaxe (p) bzw. die doppelte Parallaxe (2p) - je nachdem, ob im Abstand von 3 oder 6 Monaten gemessen wurde. Die Entfernung des Sterns ergibt sich danach aus der einfachen Formel

Wahrscheinlich werden wir aber schon froh sein müssen, die Fixsternparallaxe überhaupt nachweisen zu können! Außerdem mag die Eigenbewegung des Sterns das Resultat maskieren bzw. verfälschen.

Von einigen Glanzlichtern abgesehen, dominieren Zwergsterne unsere unmittelbare kosmische Nachbarschaft (der im Artikel verwendete Begriff "Grätzl" bezeichnet in Wien eine kleinräumige städtische Struktur, etwa die Summe der nächstgelegenen Häuserblocks).

Unsere "Grätzl-Gnome" sind lichtschwach und entsprechend schwer zu beobachten. Mit Hilfe der Himmelsfotografie können aber meist auch Amateure diese Nachbarn erfassen. Die allernächsten Sterne eignen sich nämlich auch am besten, um die Fixsternparallaxe nachzuweisen.

Diese hier angeführten Termine ermittelte ich, indem ich mit Guide 9.1 die Konjunktion des jeweiligen Sterns zur Sonne gesucht habe (dort definiert als geringster Winkelabstand zwischen den beiden am Himmel).

Der Morgenhimmel-Termin wurde von mir dann ganz simpel 3, die Opposition 6 und der Abendhimmel-Termin 9 Kalendermonate nach der Konjunktion angesetzt.

Diese Termine stimmen wegen der leicht elliptischen Form der Erdbahn und der etwas unterschiedlichen Monatslängen natürlich nicht ganz genau. Abweichungen von einigen Tagen werden bei unseren begrenzten Messmöglichkeiten aber keinen nachweisbaren Einfluss aufs Ergebnis haben.

Zwei nahe, aber äußerst lichtschwache Braune Zwerge habe ich in der folgenden Auflistung außen vor gelassen.

Proxima, Alpha A und B Centauri im Sternbild des Kentauren

• Ein Roter Zwerg und zwei Haupreihensterne umkreisen einander
  
• Entfernung 4,24 bzw. 4,34 Lichtjahre, Parallaxe 0,77 bzw. 0,75"
  
• Leider hebt sich das Trio nie über den österreichischen Horizont
  

Barnards Pfeilstern im Sternbild Schlangenträger

• Roter Zwerg, Helligkeit 9,5 mag. Ein sehr, sehr enger Doppelstern
  
• Weitere Namen (je nach Katalog): BD +4° 3561a, GJ 699, HIP 87937
  
• Entfernung: 6,0 Lichtjahre, Parallaxe 0,547 Bogensekunden
  
• 6 Monate: um den 21.3. (morgens) und um den 21.9. (abends)
  
• 3 Monate: ein obiger Termin plus Opposition um den 21.6. (nachts)
  

Wolf 359 im Sternbild Löwe

• Roter Zwerg, Helligkeit 13,5 mag
  
• Andere Namen: GJ 406, CN Leonis, LHS 36, G 45-20
  
• Entfernung 7,8 Lichtjahre, Parallaxe 0,42 Bogensekunden
  
• 6 Monate: um den 5.12. (Morgenhimmel) und um den 5.6. (Abendhimmel)
  
• 3 Monate: ein obiger Termin plus Opposition um den 5.3. (ganze Nacht)
  

Lalande 21185 im Sternbild Großer Bär

• Roter Zwerg, Helligkeit 7,5 mag hell. Eigentlich ein sehr enger Doppelstern
  
• Andere Bezeichnungen: BD +36° 2147, HD 95735, GJ 411 bzw. HIP 54035
  
• Entfernung 8,3 Lichtjahre, Parallaxe 0,39 Bogensekunden
  
• 6 Monate: um den 25.11. und um den 25.5. (zirkumpolar)
  
• 3 Monate: ein obiger Termin plus Opposition um den 25.2. (ganze Nacht)
  

Sirius im Sternbild Großer Hund

• Hauptreihenstern, der hellste Fixstern
  
• Andere Bezeichnungen: Alpha Canis Majoris, Sirius A
  
• Entfernung 8,6 Lichtjahre, Parallaxe 0,38 Bogensekunden
  
• Sirius A ist zu hell, um ihn ganz sicher zu astrometrieren
  
• Der Begleitstern Sirius B, ein Weißer Zwerg, wird von Sirius A überstrahlt
  
• 6 Monate: um den 5.10. (Morgenhimmel) und um den 5.4. (Abendhimmel)
  
• 3 Monate: ein obiger Termin und zur Opposition um den 5.1. (ganze Nacht)
  

Luyten 726-8 im Sternbild Walfisch

• Zwei Rote Zwerge umkreisen hier einander, gemeinsame Helligkeit 12,1 mag
  
• Andere Namen: UV Ceti, WDS J01388-1758AB, GJ 65
  
• Entfernung 8,7 Lichtjahre, Parallaxe 0,37 Bogensekunden
  
• 6 Monate: um den 6.7. (Morgenhimmel) und um den 6.1. (Abendhimmel)
  
• 3 Monate: ein obiger Termin und zur Opposition um den 6.10. (ganze Nacht)
  

V1216 Sgr im Sternbild Schütze

• Roter Zwerg, Helligkeit 12,6 mag
  
• Andere Namen: CD −23° 14742, GJ 729, HIP 92403, Ross 154
  
• Entfernung 9,7 Lichtjahre, Parallaxe 0,34 Bogensekunden.
  
• 6 Monate: um den 1.4. (Morgenhimmel) und um den 1.10. (Abendhimmel)
• 3 Monate: ein obiger Termin und zur Opposition um den 1.7. (ganze Nacht)
  

Datum ca.   Stern                 Termin

5.1.        Sirius                Opposition

6.1.        Luyten 726-8          Abendhimmel

5.2.        Lalande 21185         Opposition

5.3.        Wolf 359              Opposition

21.3.       Barnards Pfeilstern   Morgenhimmel

1.4.        V1216 Sgr             Morgenhimmel

5.4.        Sirius                Abendhimmel

5.5.        Lalande 21185         Abendhimmel

5.6.        Wolf 359              Abendhimmel

21.6.       Barnards Pfeilstern   Opposition

1.7.        V1216 Sgr             Opposition

6.7.        Luyten 726-8          Morgenhimmel

21.9.       Barnards Pfeilstern   Abendhimmel

1.10.       V1216 Sgr             Abendhimmel

5.10.       Sirius                Morgenhimmel

6.10.       Luyten 726-8          Opposition

25.11.      Lalande 21185         Morgenhimmel

5.12.       Wolf 359              Morgenhimmel

Das folgende Verfahren bietet eine Möglichkeit:

Man macht zunächst eine Belichtungsreihe, um die Zeiten für eine kurze und eine ausreichend lange Belichtung zu ermitteln. Dann schießt man, in möglichst rascher Folge, eine eher kurz-, eine ausreichend lang- und nochmals eine eher kurzbelichtete Aufnahme.

Die beiden eher kurzbelichteten Bilder werden mit einem Fotoeditor untersucht. Damit ermittelt man die x- und y-Koordinaten des hier kleinen Sterns (x1 und y1 aus der ersten, x2 und y2 aus der zweiten Aufnahme). Die x,y-Koordinaten werden zumeist auf der unteren Leiste angezeigt.

Im Idealfall sind sie auf beiden Aufnahmen gleich. Weichen sie nur um 1 bis 3 Pixel voneinander ab, bildet man das mathematische Mittel:

• xm = (x1 + x2) / 2
  
• ym = (y1 + y2) / 2

Nun öffnet man die langbelichtete Aufnahme mit dem selben Fotoeditor und trägt auf dem hier fett abgebildeten Sirius einen feinen schwarzen Punkt ein - und zwar möglichst exakt bei den Koordinaten xm und ym.

Erst diese bearbeitete Aufnahme wird astrometriert. Bei Ausmessen richtet man den Mauszeiger auf den schwarzen Punkt und erhält so - theoretisch - brauchbare Stern-Koordinaten.

Allzu kurz sollte man aber auch nicht belichten, weil sonst die Messgenauigkeit wieder leidet. Die Luftunruhe lässt den Stern ja chaotisch ein wenig um seine mittlere Position tanzen. Belichtet man etwas länger, gleichen sich diese zufallsbedingten Abweichungen statistisch aus.